








ЧАСТЬ 2. ГРАФОВЫЕ И ПАТТЕРНОВЫЕ СЕТИ
Эпиграф.
"Математики изучают не предметы, а
только лишь отношения между ними."
Анри Пуанкаре
ЛЕКЦИЯ 6. Теория графов и графовые сети
Разделы Лекции 5: 5.1 Диаграмма прецедентов, 5.2 Проектирование баз данных, 5.3 Другие диаграммы компьютерной системы Истерн.
6.1. Графы как модели сложных систем.
В предыдущих лекциях вы узнали, что язык UML предназначен для моделирования и инженерного проектирования компьютерных систем и их программных средств. При этом подчеркивалось, что компьютерная система в целом и ее программное обеспечение являются сложными системами. Кстати, наш веб-курс также представляет собой сложную систему. Поскольку понятие "сложная система" играет важную роль в современной компьютерной практике рассмотрим его подробнее. Говоря просто, сложная система - это такая, которую нельзя понять рассматривая ее только с одной точки зрения и отобразив эту точку зрения в виде наглядной модели (рисунка на бумаге) или в виде математической модели, взаимосвязанной с наглядной моделью. Чтобы осмыслить многие аспекты, необходимые для решения задачи проектирования сложной системы, ее разработчики должны рассматривать эту систему с нескольких точек зрения. Практика показала, что разработчикам иногда приходится отображать отдельную точку зрения на сложную систему не одной, а несколькими моделями. Различные точки зрения на систему и все отображающие эти точки зрения модели объединяются в проектной документации и в умах разработчиков в единое (интегральное) представление о системе.
Модель, отображающую точку зрения на систему, называют "видом" или "взглядом" (view). Итак мы установили, что точка зрения на сложную систему может отображаться одной моделью или двумя моделями, одна из которых наглядная, а другая, взаимосвязанная с ней математическая. Кроме того, отметим, что одна точка зрения на сложную систему может отображаться в трех и более моделях.
Разработчики сложной системы, когда они рассматривают ее с разных точек зрения и строят для каждой точки зрения модели (виды), действуют примерно также как инженер-конструктор, который рассматривает с разных точек зрения сложную деталь изделия и чертит на бумаге ее виды - "вид прямо", "вид сверху", "вид сбоку" и дополнительные виды по стрелкам А,Б и другим.
В дальнейшем мы будем иметь дело с модульными, графовыми, табличными и теоретико-множественными моделями (взглядами) на сложные системы. Все эти модели опираются на соответствующие теории; модульные модели опираются на дискретную теорию паттернов, графовые - на теорию графов, табличные - на алгебру отношений, теоретико-множественные - на теорию множеств. Модульные, графовые и табличные модели сложных компьютерных систем представляются в двух формах - в виде наглядных моделей (схем, диаграмм, таблиц) и в виде взаимосвязанных с ними математических моделей. Наглядные модели сложных систем очень важны для практики, поскольку ими могут пользоваться в практических целях люди, не имеющие представления о математических моделях, на которые опираются эти наглядные модели.
Рассматривая язык UML мы отмечали, что он опирается на теорию множеств и теорию графов. Мы не будем затрагивать теорию множеств, а рассмотрим только теорию графов, поскольку она позволяет создавать наглядные модели сложных систем, понятные широкому кругу людей. Но прежде чем начать рассказ о теории графов, объясним необходимое для ее понимания математическое понятие "бинарные отношения".
6.2. Бинарные отношения
В теории графов применяется математическое понятие, называемое "отношение". В математике отношение определяет некоторую связь между двумя предметами (объектами). В идеальном мире (существующим в сознании людей) и в реальном (физическом) мире существуют разнообразные отношения между предметами. Поэтому математики и специалисты в области компьютеров используют множество различных бинарных (двуместных) отношений. Бинарные отношения могут иметь имена, например "равенство", "отношение порядка" и т.п. Некоторые из бинарных отношений помимо имен имеют стандартные символьные обозначения. Примерами, таких отношений являются "равенство" (стандартное обозначение =), отношения "больше, (>)" и "меньше,(<)" и ряд других отношений.
В общем случае бинарные отношения обозначаются символом . Словосочетание "в общем случае" следует понимать как "все бинарные отношения". Выражение "в общем случае" будет часто встречаться в нашем Курсе в разных контекстах. Кроме бинарных существуют n-арные отношения, но они, в отличие от бинарных отношений, не имеют общего символьного обозначения. Заметим, что n-арные отношения широко используются в теории реляционных баз данных.
Любое бинарные отношение представляется множеством упорядоченных пар элементов. В математике множество элементов обозначается с помощью двух фигурных скобок { }, а упорядоченная пара с помощью символов < >. Множество {<2,4>,<7,3>,<3,3>}, будучи множеством, состоящим из трех упорядоченных пар, есть бинарное отношение. Пара <2,4> является элементом этого бинарного отношения. Элемент бинарного отношения, т.е. упорядоченную пару в общем случае обозначим Поскольку бинарные отношения постоянно встречаются в математике и науке о компьютерах, то, часто, прилагательное "бинарное" опускается и вместо словосочетания "бинарное отношение" говорят просто "отношение".
Рассмотрим теперь бинарные отношения, записываемые не в числовом виде, а с помощью слов. Пусть имеется множество, состоящее из двух словесных элементов {"отец-Иван", "сын Ивана-Николай"}. Установленное на нем полное бинарное отношение состоит из двух упорядоченных пар - <отец-Иван, сын-Николай> и <сын-Николай, отец-Иван>. Поименованные бинарные отношения используются в реляционных базах данных.
Математики рассматривают отношения с двух точек зрения. Иногда, они смотрят на них как на самостоятельные объекты. В других случаях они используют отношения совместно с множествами элементов, на которых эти отношения устанавливаются.
6.3. Теория графов
Теория графов и графовые сети (или просто графы) используются практически во всех областях знаний, в том числе, в компьютерной науке и практике. В частности, большую часть UML диаграмм можно представить графами. Основное достоинство графов в том, что их можно рисовать на бумаге или экранах компьютеров в виде точек соединенных стрелками и/или линиями. Вместе с тем, связанный граф представляется формально с помощью наборов бинарных отношений и/или множеств, каждое их которых состоит из двух элементов. Графы рисуют на бумаге не только те кто понимают теорию графов, но и люди, которые никогда о ней не слышали. К примеру, любой администратор, изображающий структуру, подчиненных ему подразделений в виде прямоугольников и стрелок между ними, по сути дела, рисует связанный ориентированный граф, хотя он и не знает об этом.
Началом теории графов считается 1736 год, когда вышла в свет статья Эйлера с его знаменитыми рассуждениями о Кенигсбергских мостах. Затем около 100 лет эта статья оставалась единственной, а методы теории графов невостребованными практикой. Интерес к графам появился только в середине 19 века благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. С тех пор сфера применений теории графов непрерывно расширялась и сегодня она представляет собой мощную формальную систему, имеющую необозримое множество областей практического применения. Естественно, в одной лекции невозможно детально рассмотреть все аспекты теории графов. Поэтому мы поступим иначе и постараемся понять ее сущность повторив ход рассуждений Эйлера о Кенигсбергских мостах.
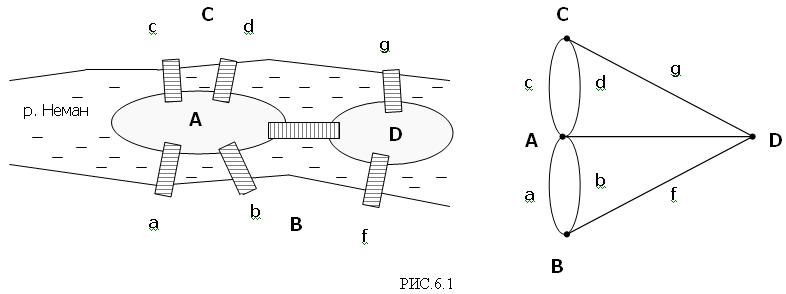
Итак в Кенигсберге (ныне г. Калининград) течет река Неман. Она омывает два острова. Между берегами реки и островами во времена проживания в Кенигсберге Эйлера существовали 7 мостов, расположение которых показывает план на Рис. 6.1.
Задача Эйлера состояла в том, чтобы определить, можно ли выйдя из пункта С (или любого другого пункта) пройти каждый мост только по одному разу и вернуться в исходный пункт. Рассуждения и действия Эйлера в ходе решения этой задачи можно представить последовательностью следующих шагов: 1) он нарисовал план, 2) нарисовал неориентированный граф, ассоциированный с берегами,
островами и мостами, 3) абстрагировал ассоциированный с данными граф от его содержания (см. Рис.6.1.б); это решающий шаг рассуждений Эйлера, поскольку абстрактный граф можно ассоциировать с чем угодно, например с площадями и улицами между ними, 4) сформулировал и доказал следующую теорему - Конечный граф G является эйлеровым графом тогда и только тогда, когда:
Любой граф может быть нарисован на бумаге или экране компьютера и представлен формально. Поэтому нарисованный на экране компьютера граф может быть транслирован в память компьютера. Покажем каким образом графы рисуются на бумаге и представляются формально на примере трех простейших графов, каждый из которых состоит из одного ребра. Они показаны на Рис. 6.2.
Четыре задачи для домашнего решения:
Поясним, что число ребер, инцидентных одной вершине графа, называется локальной степенью в этой вершине. Мы не будем доказывать эту теорему, которая является второй частью рассуждений Эйлера.
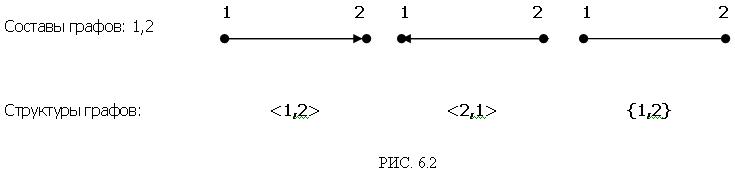 Рис.6.2 раскрывает сущность теории графов в наглядной и
формальной формах.
Рис.6.2 раскрывает сущность теории графов в наглядной и
формальной формах.